[cs224n] 2강 워드 벡터와 워드 센스 (1/5, 워드 벡터와 워드2벡 (word vector, word2vec))

지난 시간 끝날때, 파이썬 노트북으로 워드 벡터를 할 수 있는 걸 보여줬죠. 시간이 모자랐는데요. 마지막 부분을 먼저 몇 분 더 보겠습니다.

GloVe 워드 벡터를 더 얘기해 보죠. 벡터 공간에서 기본적인 유사성을 보여주는 결과들이 있어서 비슷한 단어 찾기에 유용하죠. 더 깊고 심오한 방법으로 의미를 잡아내기도 합니다. 공간속에 어떤 의미를 갖는 지점으로 가리키는 방향이 있고, 그래서, 어떤 방향을 가리키면, 이게 그 경우고, 다른 방향을 가리키면, 이건 그 나라의 수도라는 등 여러 다른 의미들이 이 공간에서 인코딩 될 수 있다는 거죠. 이 비유 (analogy)를 테스트 방법으로사용하는 건데요. 아이디어는 쌍으로 된 단어들을 사용해서요. 왕과 남자 같은거죠. 왕의 벡터가 있고, 남자 벡터가 있다면, 우리는 벡터 빼기처럼 빼보는 거죠. 선형대수시간에 배운 것 처럼요. 왕 벡터에서 남자 벡터를 빼면, 머릿속에 드는 생각은 아마 남은 것은 왕의 신분일거라는거고, 남자다움은 없는거죠. 여자 벡터가 있는데, 아까의 결과에 여자 벡터를 더하면, 어떤 벡터의 지점으로 가서 거기에서 찾을 수 있는 가장 가까운 단어를 출력하는거죠. 지난시간에 봤듯이, 여왕을 볼 수 있죠. 지난시간에 국적과 관련된 것들을 보여줬죠. 놀랍고 충격적인 것은, 이 공간에서 의미를 얻을 수 있는 모든 것에서 동작한다는 겁니다.

다양한 비유 질문을 할 수 있는데, 호주와 맥주 관계는 프랑스의 뭘까요? 샴페인이네요. 좋은 답이죠.

구문적인 것도 할 수 있는데, 큰과 가장 큰 건은 긴 것과 가장 긴 것이죠. 좋은 것과 환상적인 것의 관계는 나쁜 것과 끔찍한 것의 관계입니다. 좀더 극단적인 방향으로 가는 의미를 잡아낸 것 같네요.

하나를 건너 뛰었는데, 오바마 대 (vs.) 클린턴은 레이건 대 닉슨이네요. 이 지점에서 알아챘을 것 같은데, 클린턴이 좀 애매하죠? 빌도 있고 힐러리도 있죠. 이건 좀 오래된 데이타라서, 2014년에 만들어져서, 이건 트럼프가 정치인으로서는 없습니다. 클린턴 둘 다 있겠지만, 2014년 데이타라는 증거로서는 저 답이 말은 됩니다. 빌 클린턴이 훨씬 많았겠죠. 그래서 클린턴과 닉슨이 약간 탄핵 당할 위험에 처한 비슷한 인물로 보이네요. 이건 우리가 어떤 문제를 갖고 있는 것처럼 보이네요. 'Clinton'이라는 문자열의 가능한 의미이죠. 빌과 힐러리 클린턴은 가까이 있을 텐데, 여러분은 클린턴이라는 친구가 있을 지도 모르죠. 다 섞여서 클린턴이라는 거죠. 이런게 문제가 있어 보이네요. 이것이 워드 벡터에서 논의하는 내용입니다. 나중에 다시 보죠.

단어 집합에 이상한 것이 있는데, 여러분이 중학교 때 이런 퍼즐을 했는 지도 모르겠네요. 시리얼이 집합에서 이상한 거죠. (결과가) 괜찮아 보이네요.

또 보여주고 싶은건, 주성분 분석 (Principal Component Analysis) 스캐터 플롯 (scatter plot)인데, 단어 집합을 만들고, 스캐터 플랏을 그립니다. 잘 동작하죠, 와인 샴페인이 가까이 있고, 차와 커피가 여기 있죠. 나라들이 여기 있고, 여기 학교, 단과 대학, 대학이 있죠. 동물들은 여기 아래에 있죠. 음식은 저깄네요. 2차원에서 유사성을 잘 보여주네요. 어느 정도는요. 100차원을 2차원으로 사영한 거라서, 주요 기학학적 특징만 보여줄 뿐 많은 정보들을 잃습니다. 가까이에 있는 것은 원래 공간에서 가까이 있을 수도 있지만 2차원으로 사영하면서 제 위치를 잃어버린 단어 들일 수도 있습니다. 이걸 너무 과신하면 안됩니다. 여러분이 이런 인포비쥬 (infoviz, 인포그래픽 의미로 보임) 같은데 관심있다면 어떻게 이런 거리를 더 정확하게 표현 할 수 있는지 생각해 봐야 합니다. 이건 매우 간단한 건데, 행렬의 차원을 줄이기 위해 PCA를 썼죠. 이 단어 벡터들도 트랜스폼하고 출력하는거죠. 스캐터 플롯에서 포인트를 레이블하고 싶었는데 방법을 모르겠어서 텍스트를 플롯팅해서 약간 떨어뜨려서 출력햇죠. 그래서 보다시피 충돌하는 것들이 보이네요. IPython notebook을 더 이상 쓰지 않을 거고 컴퓨터가느려지는게 싫으면 노트북을 끄세요.

워드 벡터로 할 수 있는 것들을 더 얘기해 보죠. 워드 센스에 대해서도 좀 애기하구요. 자세히는 워드2벡에 대해서 얘기하고, 최적화에 대해 간단히 알아보고, 그 다음 공간에 대해서 설명하고 싶은데요. 밀도높은 단어 표현으로 사람들이 여태 한 것과 할 수 있는걸요. 의미를 잡아내기 위한 카운트 기반 접근방법 (count based approach)이 어떻게 동작하는지 얘기할 겁니다. GloVe 모델을 포함한 워드 벡터의 여러 모델에 대해서 얘기하죠. 저와 제프리 페닝턴의 포닥 내용이죠. 몇 년전 했는데, 평가 (evaluation)에 대해 얘기할 건데, 우리가 하는 자연어 처리에 있어서 이건 지배적인 주제입니다. 어떻게 우리가 평가하는 지, 우리가 얼마나 평가를 신뢰하는 지는요. 그 다음 워드 센스에 대해 얘기할 겁니다. 수업 말미에, 여러분이 이 지형을 이해할 수 있도혹 하는 것이 제 목표니다. 여러분들이 강의 계획표에 있는 워드 벡터에 대한 논문을 읽을 수 있고, 그것들이 어디서부터 나왔고 어떻게 동작하는지에 대해서 이해할 수 있도록 하는 거죠. 이 클래스의 공부를 최소화하고 싶다면, 첫주 후 내가 아는 것은 워드 벡터에 대한 기말 프로젝트를 할거고 나는 괜찮을 거라는 것입니다. 워드 벡터로 작업하는 것은 꽤 조심해야 할 영억이죠. 여러분은 분명 더 실력이 나아질 것입니다. 그리고 수업 뒷부분도 듣는 거죠.

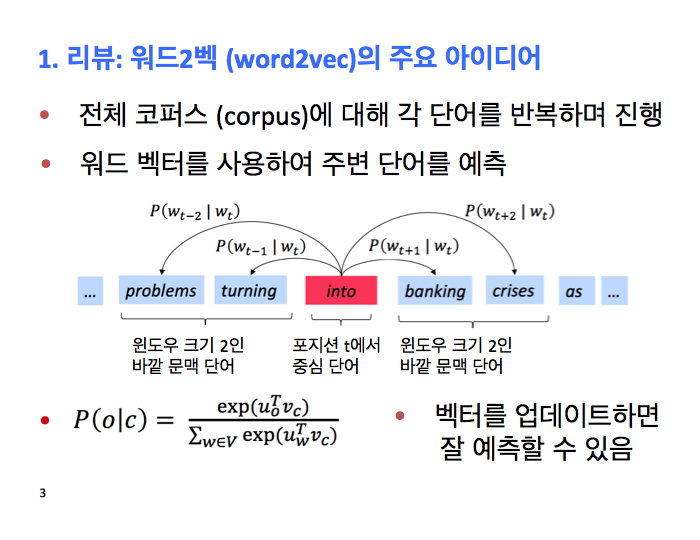
우리는 워드2벡 아이디어를 배웠는데, 반복적으로 업데이트하는 알고리즘으로 단어에 대한 벡터 표현을 학습하는 거죠. 어떤 의미에선, 단어의 의미를 잡아냅니다. 그게 동작하는 방식은 코퍼스 전체를 포지선 마다 이동하면서 각각의 포인트에서 우리는 중심 단어를 가지고 있고 주변 단어들을 예측하는 겁니다. 주변에 나타날 단어들에 대해 확률분포를 가짐으로써요. 그 확률 분포는 간단히 정의되는데, 소프트맥스 (softmax) 함수를 거친 워드 벡터의 내적이죠. 우리가 하고 싶은건, 이게 좋은 확률 분포 예측을 주도록 저 벡터들을 바꾸는 거죠. 여러분이 문맥에서 보고 싶은 단어에 가능한 높은 확률을 주도록요.

좀더 파고 들어 보면, 우리가 가지고 있는 것은 2개의 행렬입니다. 우리는 단어장의 각 단어에 대한 벡터가 있는 것이죠. 텐서플로우, 파이토치, 같은 모든 딥러닝 패키지에서 워드 벡터는 행 (row)으로 표현됩니다. 여러분이 수학 수업을 많이 들었으면, 반대를 기대하고 있을 지도 모르겠네요. 모두 행으로 들어가 있습니다. 우리는 6개의 단어와 5차원 벡터를 각각을 가지고 있죠. 이 바깥 (outside) 행렬는 각 단어에 대한 두번째 벡터인데 문맥에서 이렇게 표현되죠. 우리가 이 특정 중심 단어를 가지고 있으면, 예를 들면 네번째 단어죠. 우리가 계산을 하면,  v4와 U의 각 행과 내적을 합니다. 그럼 우리는 내적 점수 벡터를 얻죠. 그리고 그 숫자들에 원소 단위로 소프트맥스를 실행합니다. 그럼 문맥에 잇는 단어들에 대해서 확률 분포가 나옵니다. 여기서 알아야 할 건, 지난시간에 알았으면 좋았을텐데요. 이번엔 반드시 알아야죠. 우리는 하나의 확률 분포만 있죠? 그래서, 우리가 예측하는 단어에 대해서, 각 지점에서 우리는 정확히 동일한 확률 분포를 예측하는 겁니다. 우리는 한칸 왼쪽 단어는 집, 세칸 옆은 집, 오른쪽 단어도 역시 집이라고 얘기하는 거죠. 맞죠? 이건 예측이 아니죠. 이건 전체적으로 볼 때 내 문맥 속에서 등장할 것 같은 단어들의 확률 분포죠. 여기서 우리가 구하는 건 이 단어의 문맥에서 상대적으로 자주 나타나는 모든 단어들에 대해 합리적으로 높은 확률 추정을 제공하는 모델입니다. 그 이상은 아닙니다. 그게 놀라운 점이죠. 이런 간단한게 결국은 단어의 의미와 단어 의미의 다양한 면을 그렇게 많이 잡아내거든요. 아이파이썬 노트북에서 보여줬던 것 처럼요. 또 얘기할 건, that이나 and나 of같이 항상 나타나는 것들에 대한 건데, 그런 모든 단어들이 높은 내적을 가져야 한다는거죠. 그런 확률을 가져야 겠죠? 첫번째 답은 "네 그게 맞습니다." 모든 워드 벡터는 그걸 반영하는 매우 강력한 확률 컴포넌트를 가집니다. 몇몇 사람들이 논의하는 것 중 하나인데요. 프린스턴 대학의 산지 아로라 (Sanjee Arora) 그룹 논문과 이 높은 빈도 효과에 대한 논문을 읽어볼 필요가 있죠 . 사실 이 높은 빈도 문제를 고치는 여러분의 조잡한 방법은 여러분의 워드 벡터에서 첫번째 가장 큰 컴포넌트가 이 빈도 효과 때문에 나온 것이고 그걸 잘라내는 거죠.그럼 여러분의 의미적 유사성을 더 잘 만들 수 있죠. 높은 빈도를 다루는 다른 방법은, 여기 아까 본 아름다운 우리의 공간이 있는데,

이 2차원 그림을 봤는데, 이건 극도록 오해를 불러 일으킵니다. 이 2차원 그림은 삼성이 노키아와 유사하다는 이런 효과들이 있죠. 여러분은 다른 이유로 노키아가 핀란드와 가까이 있도록 하는 효과도 기대할지 모르겠습니다. 여러분은 그걸 2차원 벡터 공간에서 할 수 없죠. 높은 차원의 벡터 공간의 특징은 매우 비직관적입니다. 비직관적이라는 건 단어가 다른 방향으로도 많은 단어들과 인접해 있다는 겁니다.