-
[cs231n] 11강 탐지와 분리 (Detection and Segmentation) (1/4, 의미적 분리와 전치 합성곱 (semantic segmentation & transpose convolution))AI 2021. 4. 24. 16:30

안녕하세요. 시작하겠습니다. cs23n 11강에 오신 것을 환영합니다. 오늘 우리는 탐지 (detection), 분리 (segementation)와 핵심 컴퓨터 시각 (computer vision) 작업들을 둘러싼 여러 많은 정말 흥분되는 주제들에 대해서 얘기하겠습니다.
(HyperQuest에 대한 내용은 현재 서비스가 되지 않는 것 같아서 건너뛰겠습니다.)

지난시간을 약간 복습해 보죠. 우리는 순환 신경망에 대해서 얘기했죠. 순환 신경망은 다양한 종류의 문제들에 사용될 수 있죠. 일대일 뿐만아니라, 우리는 일대다, 다대일, 다대다도 할 수 있습니다. 우리는 이것이 언어 모델링에 적용될 수 있다는 걸 봤죠.

우리는 몇 가지 멋진 예제들을 봤는데 신경망을 다양한 종류의 언어에 문자 수준 (character level)으로 적용한 것들이었죠. 이런 인공적인 수학과 셰익스피어어와 C 소스 코드를 샘플링 했죠.

우리는 또한 비슷한 것들이 이미지 캡셔닝에 적용될 수 있다는 걸 봤죠. CNN 피쳐 추출 (feature extraction)을 RNN 언어 모델과 연결해서요. 그에 대한 정말 멋진 예제들을 봤습니다.

우리는 또한 다양한 종류의 RNN들에 대해서 얘기했죠. 이 바닐라 RNN에 대해서 얘기했는데 가끔 이건 Simple RNN이나 Elman RNN이라고도 불린다는 것을 얘기하고 싶네요. 문서에서 이런 다른 용어들을 보게 될 겁니다. 우리는 또한 LSTM (Long Short Term Memory)에 대해서 얘기했죠. 그리고 LSTM이 어떻게 이런 미친 방정식 집합을 가지게 되었는지 얘기했죠. 그러나 그건 합리적이죠. 왜냐면 역전파동안 경사 흐름을 개선해 주고 이것이 순열 (sequence)에서 더 많은 더 긴 항 의존성 (more longer term dependencies)을 모델링하도록 해주니까요.

오늘 우리는 주제를 바꿔서 많은 다양한 흥분되는 작업들에 대해 얘기할 겁니다. 지금까지 우리는 주로 이미지 분류 (image classification) 문제에 대해서 얘기해왔죠. 오늘은 다양한 종류의 다른 컴퓨터 시각 작업들에 대해 얘기할 거고, 안으로 들어가서 이미지 내의 공간적 픽셀 (spatial pixels)에 대해서 얘기할 겁니다. 분리 (segmentation), 위치 찾기 (localization), 탐지 (detection)와 몇 가지 다른 컴퓨터 시각 작업을 볼 거고 합성곱 신경망으로 이것들을 어떻게 접근할 것인지 보겠습니다.
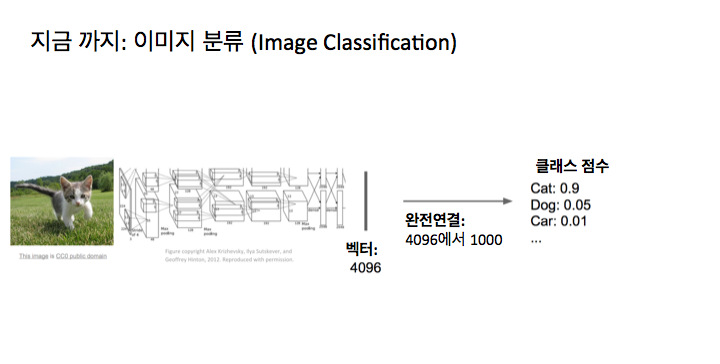
약간 기억을 되살려 보면, 지금까지 우리가 이 수업에서 주로 얘기한 것은 이미지 분류였죠. 그래서 여기 어떤 입력 이미지가 들어올 거고 그 입력 이미지가 어떤 깊은 합성곱 망을 통과할 거고 그 망은 아마 4096 차원의 피쳐 벡터를 제공할 겁니다. 알렉스넷 (AlexNet)이나 VGG경우에는요. 그 최종 피쳐 벡터로부터 우리는 어떤 완전 연결 계층을 가질 거고 그건 여러 클래스들에 대해 1000개의 점수를 주죠. 그게 우리가 신경쓰는 건데 1000은 아마도 이 예에선 이미지넷의 클래스 숫자겠죠. 마지막에는 이 망 (network)은 이미지를 입력하면 하나의 카테고리 레이블 (category label)을 출력하면서 이 전체 이미지의 내용이 전체적으로 무엇인지를 얘기하는 거죠. 그러나 이것은 아마도 컴퓨터 시각에서 가장 기본적이고 가능한 작업일 겁니다. 그런데 우리가 딥러닝 (deep learning)을 사용해서 풀고 싶은 많은 다른 재밌는 종류의 작업이 있죠.

오늘은 이 여러 작업들 중 몇 가지에 대해서 얘기할 거고 이것들의 각각을 차례대로 보고 그것들이 어떻게 딥러닝으로 동작하는지 보죠. 그래서 이것들에 대해서 각 문제가 어떤 것인지 들여다 보면서 더 자세히 얘기할겁니다. 이건 일종의 요약 슬라이드인데요. 먼저 의미적 분리 (semantic segmentation)에 대해서 얘기할 겁니다. 분류 + 위치 찾기에 대해서도 얘기할 거고 그다음 물체 탐지와 마지막으로 인스턴스 분리 (instance segmentation)에 대해 몇 마디 할 겁니다.
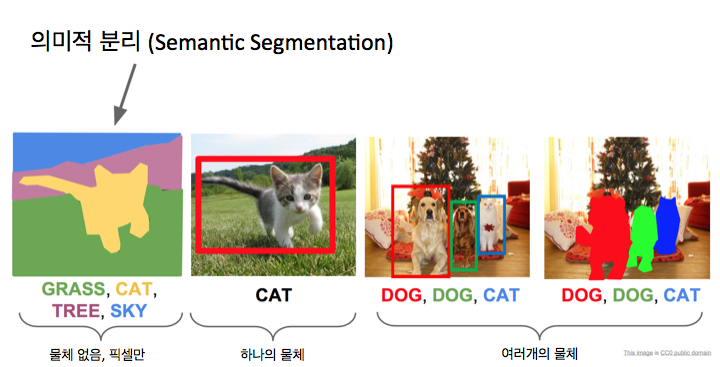
먼저 의미적 분리 문제입니다.의미적 분리 문제에서는 이미지를 입력하고 모든 픽셀에 대해 카테고리를 결정하고 싶은 겁니다. 이것이 예제 이미지 인데요. 이 고양이는 들판을 걷고 있고, 매우 귀엽죠. 출력에서 우리는 모든 픽셀에 대해 저 픽셀은 고양이, 잔디, 하늘, 나무 혹은 배경이라고 얘기하고 싶은거죠. 그래서 우리는 몇가지 카테고리 집합을 가지고 있을 겁니다. 이미지 분류에서 그랬듯이요. 그러나 이제 하나의 카테고리 레이블을 전체 이미지에 부여하는 대신 입력 이미지의 모든 픽셀에 대해서 카테고리 레이블을 만들어 내고 싶은 거죠. 이걸 의미적 분리라고 부릅니다.

의미적 분리에서 재미있는 것은 인스턴스 (instance)를 구별하는 것이 아니라는 겁니다. 오른쪽 예에서 우리는 소 두마리가 있는 이 이미지가 있는데요. 그 둘은 서로 바로 옆에 있지만, 의미적 분리를 얘기할 때는 그 픽셀의 카테고리가 무엇인지에 대해서 독립적으로 모든 픽셀에 레이블링을 하는 거죠. 그래서 이것과 같은 경우에 우리는 소 두마리가 바로 옆에 있지만, 출력은 이 두마리 소를 구별하지 않죠. 그대신, 우리는 모두 소로 레이블된 전체 픽셀 덩어리를 얻습니다. 그래서 이것이 의미적 분리의 단점이라고 할 수 있는데, 나중에 인스턴스 분리에 갔을 때, 이것을 어떻게 고칠 수 있는지 보겠습니다. 적어도 지금은 그냥 의미적 분리를 먼저 얘기하겠습니다.

의미적 분리를 공격하기 (attack) 위한 하나의 잠재적인 접근법은 분류를 통한 방법일 겁니다. 여려분은 이 슬라이딩 윈도우 (sliding window) 접근 방법 아이디어를 의미적 분리에 사용할 수 있을 겁니다. 입력 이미지를 받아서 그 이미지를 많고 많은 작고 작은 지역으로 잘라낸 조각으로 분해할 수 있죠. 이 예에서는, 아마도 소의 머리 주변으로부터 3개의 잘라내기를 해서 그걸 분류 문제로 다루는 것을 생각할 수 있는 거죠. 이 잘라내기를 예로 들면, 그 잘라낸 조각의 중심 픽셀은 무슨 카테고리인가요? 그다음 우리는 우리가 전체 이미지를 분류하기 위해 개발한 그 기계 (machinery)를 모두 사용할 수 있습니다. 그러나 이제는 전체 이미지에 대해서가 아니라 잘라낸 것들에 대해서 적용하는 거죠. 이건 아마도 어느 정도까지는 동작하겠지만 아마도 좋은 아이디어는 아닙니다.

이건 결국 수퍼 수퍼 계산적으로 비싼 것이 되고 말 겁니다. 왜냐면 이미지의 모든 픽셀을 레이블하려고 할거기 때문에, 우리는 저 이미지의 모든 픽셀에 대해 별도의 잘라내기가 필요할 거고 그건 순방향과 역방향 전달하기가 수퍼 수퍼 비싼것이 되는 거죠. 게다가, 이걸 생각해 보죠. 우리는 사실 여러 조각들 사이에 계산을 공유할 수 있습니다. 만약, 서로 바로 옆에 있어서 겹치는 2개의 조각을 분류하려고 하면, 그 조각들의 합성곱 피쳐들은 결국 같은 합성곱 계층을 거치게 될 거고 이것을 별도의 전달에 적용할 때나 이런 종류의 접근 방법을 별도의 이미지 조각들에게 적용하려고 할 때, 우리는 사실상 많은 계산을 공유할 수 있을 겁니다. 이건 사실상 끔찍한 아이디어고 아무도 하지 않죠. 여러분도 아마 하지 말아야 겠죠. 그러나 적어도 그건 의미적 분리를 생각하려고 한다면 적어도 먼저 생각해 볼 수 있는 것일 겁니다.

다음 아이디어는 약간 더 잘 동작 하는데, 완전 합성곱 망 (fully convolutional network) 아이디어 입니다. 개별적인 조각을 이미지로부터 추출하고 이 조각들을 독립적으로 분류하기 보다는, 망이 전체 거대한 합성곱 망을 쌓은 것이라고 생각할 수 있죠. 완전 연결 계층같은 것은 없죠. 이 경우 우리는 그냥 많은 합성곱 계층이 있고, 그것들은 마다 3 x 3에 0 패딩 정도죠. 그래서 각각의 합성곱 계층은 입력의 공간적 크기를 유지하죠. 우리의 이미지를 이 전체 합성곱 계층 스택에 통과시키면, 최종 합성곱 계층은 그냥 C x H x W의 어떤 텐서 (tensor)를 출력할 겁니다. 여기서 C는 우리가 신경쓰는 카테고리의 숫자죠. 여러분은 이 텐서를 입력 이미지의 모든 지점에서 입력 이미지의 모든 픽셀에 대해 분류 점수를 주는 것이라고 생각할 수 있죠. 그리고 우리는 이 모든 것을 어떤 거대한 합성곱 계층을 쌓은 것으로 한번에 계산할 수 있을 겁니다. 그다음 이것을 훈련시킬 때, 이 출력의 모든 픽셀에서 분류 손실을 넣는 것을 생각할 수 있죠. 공간에서 저 픽셀들에 대해 평균을 내는 거죠. 그리고 그냥 일반적인 보통의 역전파 (backpropagation)를 통해 이런 종류의 망을 훈련시키는 겁니다.

그러나 그건 문제인 것 같네요. 이 셋업 (setup)에서는 입력 이미지의 같은 공간 크기를 유지하는 많은 합성곱을 적용하기 때문에, 이건 수퍼 수퍼 비싸게 됩니다. 만약 저 합성곱 필터에 대해 64, 128, 혹은 256 채널을 가진 합성곱을 하려고 한다면, 그건 이런 많은 망 들에서 꽤 흔한데요, 이 고해상도 입력 이미지에 대해서 저런 합성곱을 일련의 계층에 걸쳐서 실행시키는 것은 극도로 계산적으로 비쌀 겁니다. 엄청난 메모리를 요구하죠. 그래서 실제에선, 일반적으로 이런 아키텍처 (architecture)를 가진 망을 여러분은 보지 않을 겁니다.

그 대신 이런 것처럼 보이는 망들을 볼 겁니다. 여기서는 우리는 이미지내에서 어떤 다운샘플링 (downsampling)을 하고 그다음 피쳐 지도 (feature map)에서 어떤 업샘플링 (upsampling)을 하죠. 그래서 이미지의 전체 공간 해상도의 모든 합성곱을 하는 대신, 우리는 아마 원래 해상도로는 작은 수의 합성곱 망을 거칠 거고 그다음 그 피쳐 지도를 다운 샘플링하죠. 최대 풀링 (max pooling)이나 스트라이드가 있는 합성곱 (strided convolution)같은 것을 사용해서요. 다운샘플링하고 다운샘플링하고, 다운샘플링한 것을 합성곱하고, 다운샘플링한 것을 합성곱해서 분류 망과 많이 비슷해 보입니다. 그러나 차이점은 이미지 분류 셋업에서 하듯이 완전 연결 계층으로 이동하는 것이 아니라 후반부에서 우리의 예측의 공간적 해상도를 높이려고 합니다. 출력 이미지가 이제 입력 이미지와 같은 크기가 되게 하기 위해서죠. 이렇게 하면 결국 훨씬 더 계산적으로 효율적이되는데, 왜냐면 망을 매우 깊게 만들 수 있고, 망내에서 많은 계층에 대해 더 낮은 공간적 해상도에서 작업할 수 있기 때문이죠. 우리는 이미 합성곱 망에 대해 다운샘플링 예제들을 봤습니다. 우리는 스트라이드가 있는 합성곱을 하거나 다양한 종류의 풀링을 해서 망내에서 이미지의 공간적 크기를 줄일 수 있다는 것을 봤죠. 그러나 우리는 업샘플링에 대해서는 사실 얘기하지 않았습니다.

여러분이 가질 수 있는 질문은 이런 업샘플링 계층이 실제로 망 내에서 어떻게 생겼는가일 겁니다. 그리고 망내에서 피쳐 지도의 크기를 키우는 전략은 무엇인가이겠죠.

업샘플링을 위한 하나의 전략은 언풀링 (unpooling)같은거죠. 우리는 이 풀링 개념 가지고 다운샘플링할겁니다. 우리는 평균 풀링 (average pooling)과 최대 풀링 (max pooling)에 대해 얘기했는데, 평균 풀링에 대해서 얘기할 때, 우리는 각 풀링 지역의 수용장 (receptive field)내에서 일종의 공간적 평균을 취했죠. 업샘플링에 대한 하나의 비유 (analog)는 이 최근접 이웃 언풀링 아이디어죠. 여기 왼쪽에서 우리는 이 최근접 이웃 언풀링 (nearest neighbor unpooling) 예를 보는데, 입력은 아마 2 x2 그리드고 출력은 4 x 4 그리드죠. 이제 출력에서 우리는 2 x 2 스트라이드의 2개의 최근접 이웃 언풀링이나 업샘플링을 했죠. 여기서 우리는 언풀링 영역의 2 x 2 수용장에서 모든 지점에 대해 그 원소를 복제했습니다. 볼 수 있는 다른 것은 이 바늘 방석 (bed of nails) 언풀링 혹은 바늘 방석 업샘플링이죠. 다시 우리는 언풀링 영역에 대해 2 x 2 수용장이 있고 이 경우 여러분은 언풀링 영역의 하나의 원소만 제외하고 그것 모두를 0으로 만들죠. 그래서 이 경우 우리는 모든 입력을 받아서 그것들을 이 언풀링 영역의 왼쪽 위에 놓고 다른 모든 것은 0이죠. 이건 일종의 바늘 방석같은 거죠 왜냐면, 0은 매우 평평한데, 이 다양한 0이 아닌 영역의 값들에 대한 이런 튀어 나온 것들이 있으니까요.

여러분이 가끔 보는 것은 조금 전에 질문에서 언급된 건데 이 최대 언풀링 (max unpooling) 아이디어입니다. 많은 이 망들에서, 그것들은 대칭적인 (symmetrical) 경향이 있죠. 여기서 우리는 망의 다운샘플링 부분이 있고 망의 업샘플링 부분이 있어서 망의 이 두 부분 사이에 균형이 있는거죠. 그래서 가끔 이 최대 언풀링 아이디어를 보게 될 거고, 각 언풀링과 업샘플링 계층에 대해, 그건 망의 전반부에서 풀링 계층의 하나와 연결되어 있죠. 다운샘플링에서 최대 풀링을 할 때는, 우리는 사실 최대 풀링동안에 수용장의 어떤 원소가 최대 풀링을 하기 위해 사용되었는지를 기억할 겁니다. 그리고 이제 망의 나머지 부분을 통과할 때는 우리는 이 바늘 방석 같은 것을 해서 업샘플링하죠. 같은 위치에 원소들을 항상 놓기보다는, 우리는 그것을 해당하는 망에서 앞선 최대 풀링 단계에서 사용되었던 위치에 넣습니다. 설명이 명확했는지 모르겠습니다만 그림이 이해가 되길 바랍니다.
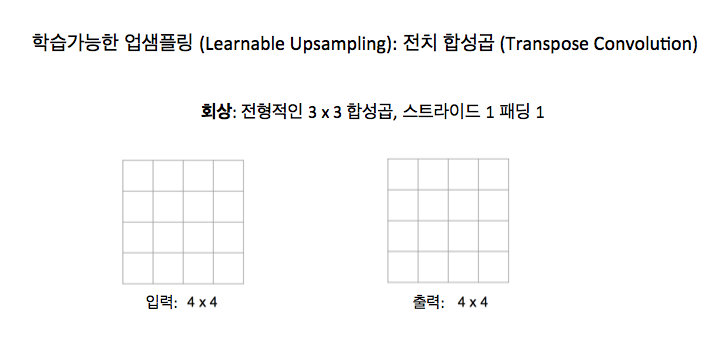
이 전치 합성곱 (transpose convolution) 아이디어를 가끔 볼게 될 겁니다. 우리가 막 얘기한 이런 다양한 종류의 언풀링, 즉, 이런 바늘 방석, 최근접 이웃, 이 최대 언풀링, 이런 모든 것들은 고정된 함수 (fixed function)죠. 그것들은 실제로는 업샘플링을 어떻게 하는 지에 대해 정확히는 학습하고 있지 않습니다. 그래서 만약 스트라이드가 있는 합성곱 같은 것을 생각해 보면, 스트라이드가 있는 합성곱은 일종의 학습할 수 있는 계층 같은 것이죠. 그건 망이 그 계층에서 다운샘플링을 수행하고 싶은 방식을 학습하는 거죠. 그것과의 비유로, 전치 합성곱이라고 불리는 이런 종류의 계층이 있는데, 그건 일종의 학습할 수 있는 업샘플링을 하게 해주죠. 그래서 그건 피쳐 지도를 업샘플링할 거고 그것이 어떻게 업샘플링을 하고 싶은지에 대한 가중치를 학습할 겁니다. 이건 정말 그냥 다른 종류의 합성곱일 뿐이죠. 이게 어떻게 동작하는지 보면, 정상적인 3 x 3 스트라이드 1 패딩 1 합성곱이 어떻게 동작하는지 기억해 보죠. 이런 종류의 일반적인 합성곱은 이 수업에서 많이 봤죠. 입력은 4 x 4 일거고, 출력도 4 x 4일겁니다.

이제 이 3 x 3 커널 (kernel)이 있을 거고 우리는 커널을 이미지의 모서리에 놓고, 내적을 취하고 그 내적은 출력의 왼쪽 위 모서리 값과 활성 (activation)을 줍니다.

우리는 이것을 이미지 내의 모든 수용장에 대해서 반복할 겁니다.

이제 스트라이드가 있는 합성곱에 대해서 얘기해 보면 스트라이드가 있는 합성곱도 결국 꽤 비슷하게 보입니다. 그러나 입력은 4 x 4 영역인데 출력은 2 x 2 영역이죠.
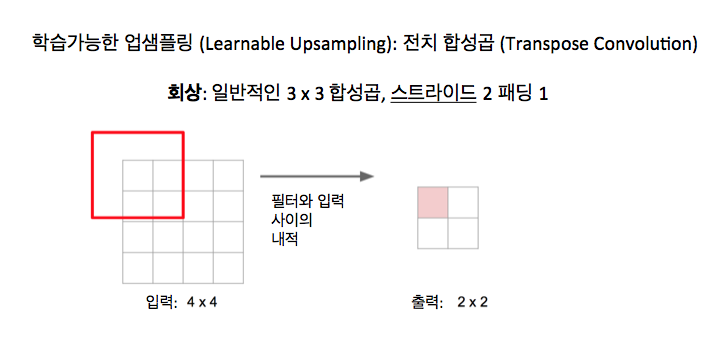
그러나 우리는 여전히 이런 아이디어가 있죠. 어떤 3 x 3 필터 혹은 커널를 이미지 모서리에 내려놓고 내적을 취하고 그걸 사용해서 활성과 출력의 값을 계산하는 아이디어 말입니다.

그러나 스트라이드가 있는 합성곱 아이디어는 입력에서 가능한 모든 지점에 필터를 내려 놓는 것이 아니라 필터를 입력에서 2 픽셀씩 움직이는 거죠. 매번 출력에서는 한 픽셀씩 움직입니다. 그래서 이 스트라이드 2는 입력에서 우리가 움직일 때 출력에서 우리가 얼마나 움직일 것인가에 대한 비율 (ratio)을 제공하죠. 스트라이드 2로 스트라이드가 있는 합성곱을 할 때, 이건 이미지나 피쳐 맵을 결국 2의 인수로 어떤 학습할 수 있는 방식으로 다운샘플링하는 것이 되죠.

이제 전치 합성곱은 어떤 면에서는 반대라고 할 수 있습니다. 여기서 입력은 2 x 2 영역인데, 출력은 4 x 4 영역이죠.

그러나 이제 전치 합성곱으로 수행하는 연산은 약간 다릅니다. 내적을 취하는 대신, 입력 피쳐 지도의 왼쪽 위 모서리 값을 취합니다. 그건 왼쪽 위 모서리의 어떤 스칼라 (scalar) 값이겠죠. 우리는 필터를 그 스칼라 값으로 곱하고 그 값들을 출력내의 이 3 x 3 영역에 복사합니다. 그래서 필터와 입력의 내적을 취하기 보다, 우리 입력은 가중치를 주는 것이고 우리는 그것을 사용해서 필터에 가중치를 줍니다. 그리고 나면 출력은 필터의 가중치가 주어진 사본이 될 거고,그건 입력내의 값들에 의해서 가중치가 주어진 것이죠.

이제 우리는 이런 종류의 같은 비율 트릭 (ratio trick)을 업샘플링하기 위해서 할 수 있습니다. 이제 입력에서 1픽셀 움직일 때, 출력에선 필터를 2 픽셀 떨어진 곳에 내려놓을 수 있는 거죠. 그건 같은 트릭이죠. 입력의 파란 픽셀이 어떤 스칼라 값이고 우리는 그 스칼라 값을 취해서 필터내의 값으로 곱하고 그 가중치가 있는 필터 값들을 복사해서 출력내의 이 새로운 영역으로 복사합니다. 까다로운 부분은 가끔 이 출력 내의 수용장이 겹칠 수 있고 이런 출력내의 수용장이 겹칠 때, 우리는 그냥 출력내에서 결과들을 더합니다.그래서 생각할 수 있듯이, 이 절차를 모든 곳에서 반복하면, 이건 결국 일종의 학습할 수 있는 업샘플링이 되는 거고, 우리는 이 학습된 합성곱 필터 가중치들을 사용해서 이미지를 업샘플링하고 공간적인 크기를 키우는 겁니다. 그런데, 이 연산이 문서에서는 다른 많은 이름으로 불리는 것을 볼 겁니다.
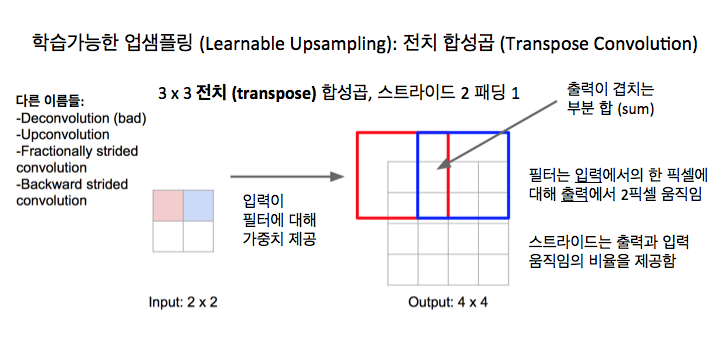
가끔 이런 deconvolution으로 불리죠. 저는 이게 나쁜 이름 같아요. 그런 여러분들은 논문에서 보게 될 겁니다. 신호처리 관점에서 보면 deconvolution 은 합성곱에 대한 반대연산인데, 이건 그게 아니죠. 그러나 자주 이런 종류의 계층이 deconvolution 계층이라고 불리는 것을 딥 러닝 논문들에서 보게 될 것이니까, 그 점에 주의하고 용어에 조심하세요. 또한 이것이 upconvolution이라고 불리는 것을 볼 텐데, 귀여운 이름이죠. 가끔 그건 fractionally strided convolution이라고 불리죠. 왜냐면 우리가 스트라이드를 입력과 출력사이의 걸음 (step)의 비율이라고 생각하면, 이건 스트라이드 1/2 합성곱인 거죠. 왜냐면 이 입력의 걸음과 출력의 걸음사이의 1/2 비율때문에 그렇습니다. 이건 또한 가끔 backwards strided convolution이라고 불리죠. 왜냐면, 그걸 생각해 보고 수학을 해 보면, 이건 결국 같은 것이되죠. 전치 합성곱의 순방향 전달 (forward pass)은 결국 일반적인 합성곱에서의 역방향 전달 (backward pass)과 같은 수학적 연산이 되죠. 여러분은 그냥 제 말을 받아들여야 할지도 모르지만, 처음 이걸 보면 그렇게 명확하진 않죠. 그러나 저 이름도 가끔 볼 거라는 것이 사실입니다.

이것이 어떻게 생겼는지에 대한 좀 더 구체적인 예로, 1차원으로 보는 것이 좀 더 쉬울 것 같습니다. 여기 우리는 3 x 1 전치 합성곱을 1차원으로 하고 있는데요. 여기 필터는 그냥 3개의 숫자죠 입력은 2개의 숫자입니다. 보다시피, 출력에서 우리는 입력의 값들을 취해서, 그것들을 사용해서 필터의 값들에 가중치를 줍니다. 그리고 이 가중치를 준 필터들을 스트라이드 2로 출력에 내려놓는 거죠. 이제 여기서 출력에서 이 수용장들이 겹치면 더합니다. 여러분들은 아마 전치 합성곱이라는 재밌는 이름 어디서 왔는지, 왜 이 이름이 사실 제가 이 연산에 대해서 제일 좋아하는 것인지를 궁금할 것 같네요.

그건 이런 합성곱에 대한 깔끔한 해석으로부터 왔습니다. 여러분이 합성곱을 할 때마다 여러분은 항상 합성곱을 행렬 곱셉으로 작성할 수 있습니다. 다시 얘기하지만, 1차원 예로 보는 것이 더 쉽죠. 우리는 가중치 벡터 x의 1차원 합성곱을 하고 있는데, x는 3개의 원소를 가지고 있고, 입력 벡터는, 즉 a, b, c, d 네개의 원소를 가지고 있는 벡터죠. 여기서 우리는 3 x 1 합성곱을 스트라이드 1로 하고 있죠. 보다시피 우리는 이 전체 연산을 행렬 곱셉으로 표현할 수 있고, 여기서 합성곱 커널 (kernel) x를 취해서 어떤 행렬 X로 변환할 수 있죠. 그건 여러 영역에 의해 오프셋 (offset)된 저 합성곱 커널의 사본을 가지고 있죠. 이제 우리는 이 거대한 가중치 행렬 X를 취해서 x와 입력간에 행렬 벡터 곱셉을 할 수 있습니다. 이건 그냥 합성곱과 동일한 결과를 만들어 내죠.

이제 전치 합성곱 (Transpose Convolution)으로 우리는 같은 가중치 행렬을 취할 거라는 것을 의미할 수 있죠. 그러나 이제 우리는 같은 가중치 행렬의 전치 핼렬로 곱하기를 하는 겁니다. 여기 왼쪽에 이 스트라이드 1의 합성곱 예제를 볼 수 있죠. 그리고 해당하는 스트라이드 1 전치 합성곱을 오른쪽에서 볼 수 있죠. 그리고 만약 세부 사항들을 연구해 보면, 스트라이드 1에 관해서는 스트라이드 1의 전치 합성곱은 또한 결국 스트라이드 1의 일반적인 합성곱이 된다는 것을 알 수 있죠. 경계와 패딩이 처리되는 약간의 세부 사항들이 있긴 하지만, 근본적으로 같은 연산입니다.

그러나 이제 스트라이드 2를 얘기할 때는 상황이 다르게 보입니다. 다시 얘기하지만, 여기 왼쪽에서 스트라이드 2인 합성곱을 취할 수 있고 이 스트라이드 2 합성곱을 행렬 곱셉으로 작성할 수 있죠.
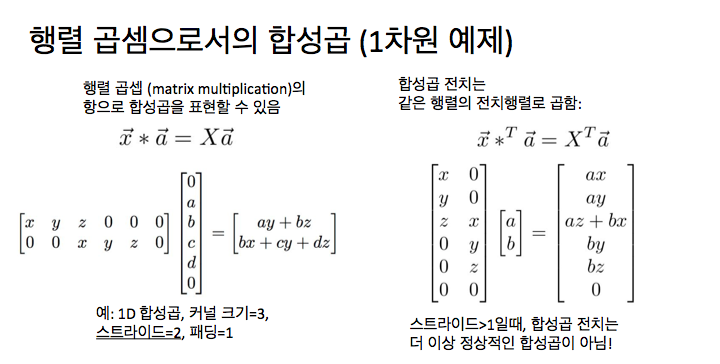
이제 해당하는 전치 합성곱은 더 이상 합성곱이 아닙니다. 이 가중치 행렬을 훑어보고 합성곱이 결국 어떻게 이렇게 표현되었는지 생각해 보면, 스트라이드 2인 합성곱에 대한 이 전치 행렬은 본래의 일반적인 합성곱과 근본적으로 다른 것입니다. 그것이 이름 뒤에 있는 논리고 이 연산을 왜 그렇게 부르는 것이 가장 좋다고 생각하는지에 대한 이유죠.

의미적 분리라는 이 아이디어는 결국 꽤 자연스러워집니다. 그냥 망 (network) 내에 다운샘플링과 업샘플링이 있는 이 거대한 합성곱 망을 가지는 거죠. 다운샘플링은 스트라이드가 있는 합성곱이나 풀링에 의해 이뤄질 거고, 업샘플링은 전치 합성곱이나 다양한 종류의 언풀링이나 업샘플링에 의해 이뤄지고 우리는 모든 픽셀에 대해서 이 교차 엔트로피 손실 (cross entropy loss)을 사용해서 이 전체를 끝에서 끝까지 (end to end) 역전파로 훈련시킬 수 있죠. 우리가 이미 이미지 분류를 위해 배운 기계 (machinery) 중 많은 것을 가지고 할 수 있다는 것은 정말 멋지죠. 그리고 이제 그걸 매우 쉽게 적용해서 새로운 종류의 문제로 확장할 수 있다는 것도 수퍼 멋지죠.
'AI' 카테고리의 다른 글